5 PCA Visualizations You Must Try On Your Next Data Science Project
Which features carry the most weight? How do original features contribute to principal components? These 5 visualization types have the answer.
Principal Component Analysis (PCA) can tell you a lot about your data. In short, it’s a dimensionality reduction technique used to bring high-dimensional datasets into a space that can be visualized.
But I assume you already know that. If not, check my from-scratch guide.
Today, we only care about the visuals. By the end of the article, you’ll know how to create and interpret:
Explained variance plot
Cumulative explained variance plot
2D/3D component scatter plot
Attribute biplot
Loading score plot
Getting Started — PCA Visualization Prerequisites
I’d love to dive into visualizations right away, but you’ll need data to follow along. This section covers data loading, preprocessing, PCA fitting, and general Matplotlib styling tweaks.
Dataset Info
I’m using the Wine Quality Dataset. It’s available for free on Kaggle and is licensed under the Creative Commons License.
This is what you should see after loading it with Python:
import numpy as np
import pandas as pd
from sklearn.preprocessing import StandardScaler
from sklearn.decomposition import PCA
data = pd.read_csv("data/WineQT.csv")
data.drop(["Id"], axis=1, inplace=True)
data.head()PCA assumes numerical features with no missing values located around 0 with a standard deviation of 1:
X = data.drop("quality", axis=1)
y = data["quality"]
X_scaled = StandardScaler().fit_transform(X)
pca = PCA().fit(X_scaled)
pca_res = pca.transform(X_scaled)
pca_res_df = pd.DataFrame(pca_res, columns=[f"PC{i}" for i in range(1, pca_res.shape[1] + 1)])
pca_res_df.head()The dataset is now ready for visualization, but any chart you make will look horrendous at best. Let’s fix that.
Matplotlib Visualization Tweaks
I have a full-length article covering Matplotlib styling tweaks, so don’t expect any depth here.
Download a TTF font of your choice to follow along (mine is Roboto Condensed) and replace the path in font_dir to match one on your operating system:
import matplotlib.pyplot as plt
import matplotlib.font_manager as font_manager
import matplotlib_inline
matplotlib_inline.backend_inline.set_matplotlib_formats("svg")
font_dir = ["Roboto_Condensed"]
for font in font_manager.findSystemFonts(font_dir):
font_manager.fontManager.addfont(font)
plt.rcParams["figure.figsize"] = 10, 6
plt.rcParams["axes.spines.top"] = False
plt.rcParams["axes.spines.right"] = False
plt.rcParams["font.size"] = 14
plt.rcParams["figure.titlesize"] = "xx-large"
plt.rcParams["xtick.labelsize"] = "medium"
plt.rcParams["ytick.labelsize"] = "medium"
plt.rcParams["axes.axisbelow"] = True
plt.rcParams["font.family"] = "Roboto Condensed"You’ll now get modern-looking high-resolution charts any time you plot something.
And that’s all you need to start making awesome PCA visualizations. Let’s dive into the first one next.
PCA Plot #1: Explained Variance Plot
Question: How much of the total variance in the data is captured by each principal component?
If you’re wondering the same, the explained variance plot is where it’s at. You’ll typically see the first couple of components covering a decent chunk of the overall variance, but that might depend on the number of features you’re starting with.
The first component of a dataset with 5 features will capture more total variance than the first component of a dataset with 500 features — duh.
plot_y = [val * 100 for val in pca.explained_variance_ratio_]
plot_x = range(1, len(plot_y) + 1)
bars = plt.bar(plot_x, plot_y, align="center", color="#1C3041", edgecolor="#000000", linewidth=1.2)
for bar in bars:
yval = bar.get_height()
plt.text(bar.get_x() + bar.get_width() / 2, yval + 0.001, f"{yval:.1f}%", ha="center", va="bottom")
plt.xlabel("Principal Component")
plt.ylabel("Percentage of Explained Variance")
plt.title("Variance Explained per Principal Component", loc="left", fontdict={"weight": "bold"}, y=1.06)
plt.grid(axis="y")
plt.xticks(plot_x)
plt.show()28.7% of total variance (from 11 features) is explained with just one component. In other words, you can plot the entire dataset on a single line (1D) and still show ~ a third of the variability.
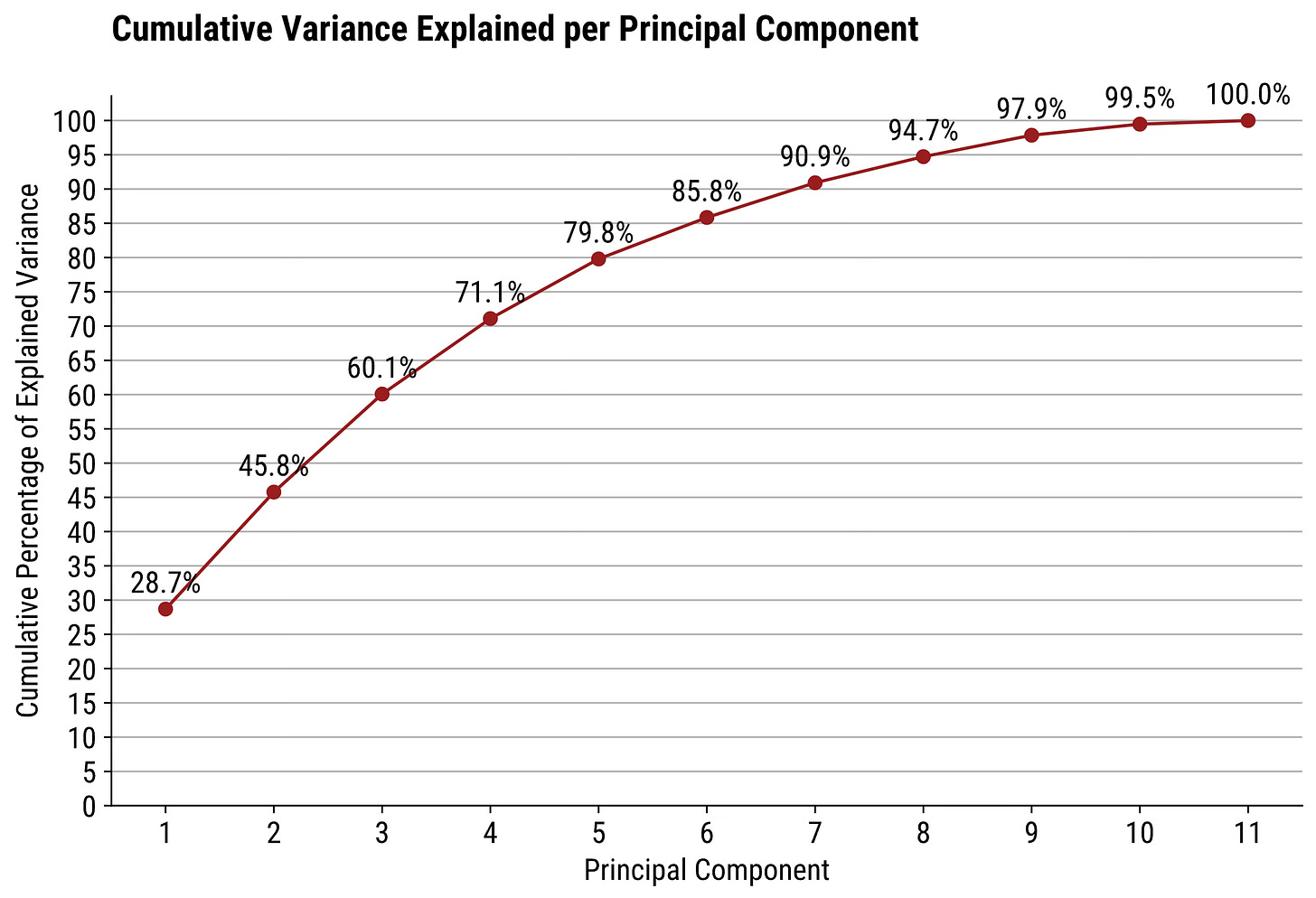
PCA Plot #2: Cumulative Explained Variance Plot
Question: I want to reduce the dimensionality of my data, but still want to keep at least 90% of the variance. What should I do?
The simplest answer is to modify the first chart so it shows the cumulative sum of explained variance. In code, just iteratively sum up the values up to the current item.
exp_var = [val * 100 for val in pca.explained_variance_ratio_]
plot_y = [sum(exp_var[:i+1]) for i in range(len(exp_var))]
plot_x = range(1, len(plot_y) + 1)
plt.plot(plot_x, plot_y, marker="o", color="#9B1D20")
for x, y in zip(plot_x, plot_y):
plt.text(x, y + 1.5, f"{y:.1f}%", ha="center", va="bottom")
plt.xlabel("Principal Component")
plt.ylabel("Cumulative Percentage of Explained Variance")
plt.title("Cumulative Variance Explained per Principal Component", loc="left", fontdict={"weight": "bold"}, y=1.06)
plt.yticks(range(0, 101, 5))
plt.grid(axis="y")
plt.xticks(plot_x)
plt.show()So, if you want a narrower dataset that still captures at least 90% of the variance, you’ll want to keep the first 7 principal components.
PCA Plot #3: 2D/3D Component Scatter Plot
Question: How can I visualize the relationship between records of a high-dimensional dataset? We can’t see more than 3 dimensions at a time.
A scatter plot of the first 2 or 3 principal components is what you’re looking for. Ideally, you should color the data points with distinct values of the target variable (assuming a classification dataset).
Let’s break it down.
2D Scatter Plot
The first two components capture ~ 45% of the variance. It’s a decent amount, but a 2-dimensional scatter plot still won’t account for more than half of it. Something to keep in mind.
total_explained_variance = sum(pca.explained_variance_ratio_[:2]) * 100
colors = ["#1C3041", "#9B1D20", "#0B6E4F", "#895884", "#F07605", "#F5E400"]
pca_2d_df = pd.DataFrame(pca_res[:, :2], columns=["PC1", "PC2"])
pca_2d_df["y"] = data["quality"]
fig, ax = plt.subplots()
for i, target in enumerate(sorted(pca_2d_df["y"].unique())):
subset = pca_2d_df[pca_2d_df["y"] == target]
ax.scatter(x=subset["PC1"], y=subset["PC2"], s=70, alpha=0.7, c=colors[i], edgecolors="#000000", label=target)
plt.xlabel("Principal Component 1")
plt.ylabel("Principal Component 2")
plt.title(f"Wine Quality Dataset PCA ({total_explained_variance:.2f}% Explained Variance)", loc="left", fontdict={"weight": "bold"}, y=1.06)
ax.legend(title="Wine quality")
plt.show()It’s a mess, so let’s try adding a dimension.
3D Scatter Plot
Adding an extra dimension will increase the explained variance to ~ 60%. Keep in mind that 3D charts are more challenging to look at, and the interpretation can somewhat depend on the chart's angle.
total_explained_variance = sum(pca.explained_variance_ratio_[:3]) * 100
colors = ["#1C3041", "#9B1D20", "#0B6E4F", "#895884", "#F07605", "#F5E400"]
pca_3d_df = pd.DataFrame(pca_res[:, :3], columns=["PC1", "PC2", "PC3"])
pca_3d_df["y"] = data["quality"]
fig = plt.figure(figsize=(10, 10))
ax = fig.add_subplot(projection="3d")
for i, target in enumerate(sorted(pca_3d_df["y"].unique())):
subset = pca_3d_df[pca_3d_df["y"] == target]
ax.scatter(xs=subset["PC1"], ys=subset["PC2"], zs=subset["PC3"], s=70, alpha=0.7, c=colors[i], edgecolors="#000000", label=target)
ax.set_xlabel("Principal Component 1")
ax.set_ylabel("Principal Component 2")
ax.set_zlabel("Principal Component 3")
ax.set_title(f"Wine Quality Dataset PCA ({total_explained_variance:.2f}% Explained Variance)", loc="left", fontdict={"weight": "bold"})
ax.legend(title="Wine quality", loc="lower left")
plt.show()To change the perspective, you can play around with the view_init() function. It allows you to change the elevation and azimuth of the axes in degrees:
ax.view_init(elev=<value>, azim=<value>)Or, you can use an interactive charting library like Plotly and rotate the chart like a sane person.
PCA Plot #4: Biplot
Question: Can I see how the original variables contribute to and correlate with the principal components?
Yup. Annoyingly, this chart type is much easier to make in R, but what can you do.
labels = X.columns
n = len(labels)
coeff = np.transpose(pca.components_)
pc1 = pca.components_[:, 0]
pc2 = pca.components_[:, 1]
plt.figure(figsize=(8, 8))
for i in range(n):
plt.arrow(x=0, y=0, dx=coeff[i, 0], dy=coeff[i, 1], color="#000000", width=0.003, head_width=0.03)
plt.text(x=coeff[i, 0] * 1.15, y=coeff[i, 1] * 1.15, s=labels[i], size=13, color="#000000", ha="center", va="center")
plt.axis("square")
plt.title(f"Wine Quality Dataset PCA Biplot", loc="left", fontdict={"weight": "bold"}, y=1.06)
plt.xlabel("Principal Component 1")
plt.ylabel("Principal Component 2")
plt.xlim(-1, 1)
plt.ylim(-1, 1)
plt.xticks(np.arange(-1, 1.1, 0.2))
plt.yticks(np.arange(-1, 1.1, 0.2))
plt.axhline(y=0, color="black", linestyle="--")
plt.axvline(x=0, color="black", linestyle="--")
circle = plt.Circle((0, 0), 0.99, color="gray", fill=False)
plt.gca().add_artist(circle)
plt.grid()
plt.show()So, what are you looking at? This is what you should know when interpreting biplots:
Arrow direction: Indicates how the corresponding variable is aligned with the principal component. Arrows that point in the same direction are positively correlated. Arrows pointing in the opposite direction are negatively correlated.
Arrow length: Shows how much the variable contributes to the principal components. Longer arrows mean stronger contribution (the variable accounts for more explained variance). Shorter arrows mean weaker contribution (the variable accounts for less explained variance).
Angle between arrows: 0º indicates a perfect positive correlation. 180º indicates a perfect negative correlation. 90º indicates no correlation.
From the above chart, you can see how the features sulphates, fixed acidity, and citric accid show a high correlation.
PCA Plot #5: Loading Score Plot
Question: Which variables from the original dataset have the most influence on each principal component?
You can visualize something known as a loading score to find out. It’s a value that represents the weight of an original variable to a given principal component. A higher absolute value indicates higher influence.
These are essentially correlations with a principal component and range from -1 to +1. You don’t often care about the direction, just the magnitude.
loadings = pd.DataFrame(
data=pca.components_.T * np.sqrt(pca.explained_variance_),
columns=[f"PC{i}" for i in range(1, len(X.columns) + 1)],
index=X.columns
)
fig, axs = plt.subplots(2, 2, figsize=(14, 10), sharex=True, sharey=True)
colors = ["#1C3041", "#9B1D20", "#0B6E4F", "#895884"]
for i, ax in enumerate(axs.flatten()):
explained_variance = pca.explained_variance_ratio_[i] * 100
pc = f"PC{i+1}"
bars = ax.bar(loadings.index, loadings[pc], color=colors[i], edgecolor="#000000", linewidth=1.2)
ax.set_title(f"{pc} Loading Scores ({explained_variance:.2f}% Explained Variance)", loc="left", fontdict={"weight": "bold"}, y=1.06)
ax.set_xlabel("Feature")
ax.set_ylabel("Loading Score")
ax.grid(axis="y")
ax.tick_params(axis="x", rotation=90)
ax.set_ylim(-1, 1)
for bar in bars:
yval = bar.get_height()
offset = yval + 0.02 if yval > 0 else yval - 0.15
ax.text(bar.get_x() + bar.get_width() / 2, offset, f"{yval:.2f}", ha="center", va="bottom")
plt.tight_layout()
plt.show()If the first principal component accounts for ~ 29% of the variability and the fixed accidity feature has a high loading score (0.86), it means it’s an important feature and should be kept for further analysis and predictive modeling.
This way, you can hack your way around loading scores to use them as a feature selection technique.
Summing up Python PCA Visualizations
To conclude, PCA is a must-know technique for reducing dimensionality and gaining insights. We humans suck at interpreting long lists of numbers, so visualization is the way to go.
Thanks to PCA, you can visualize high-dimensional datasets with 2D/3D charts. You’ll lose some variance along the way, so interpret your visualizations carefully.
Which PCA visualizations do you use in data science projects? Make sure to let me know in the comment section below.